Scaling Laws: Uses and Misuses in Industrial Plant and Equipment Replacement Cost Estimates

By Clayton T. Baumann, PE, CCP, ASA | evcValuation and Alexander Lopatnikov, ASA, RICS | American Appraisal

Click HERE to download a PDF version of this article

Abstract

Scaling laws are ubiquitous in the study of nature, biology, computer networks, economics and other social sciences,[1] and various engineering applications. They establish a relationship, often in the form of a power law, between certain key parameters and characteristics of complex systems. Scaling laws can prove to be practical tools in developing simplifications while allowing meaningful comparison or inferences to be made about the behavior of complex systems. However, as is commonly the case, the laws have tradeoffs and limitations that must be taken into consideration.

Appraisers and cost engineers often use a variation of a scaling law, known as an empirical rule or the cost-to-capacity method. This article addresses the basics of the cost-to-capacity method when applied in cost estimating or comparing replacement costs of various industrial facilities and equipment, with a specific focus on the limitations of this method that practitioners need to be aware of.

Introduction

Appraisers and cost engineers are often engaged in developing higher level assessments of replacement cost for various types of industrial plants and production units. These may vary from complex facilities such as crude oil refineries, petrochemical plants, or steel plants, to simpler and seemingly straightforward pieces of machinery or vehicles. One of the issues appraisers and cost engineers typically struggle most with in developing replacement cost estimates is identifying similar facilities to apply as benchmarks or pricing reference points. It is not unusual to find that the plant, or production unit, under consideration differs from comparable facilities in production capacity (size, power, throughput, or other parameters), even when the facilities are similar in many other respects. In such instances, an understanding of how specific plant or equipment costs scale up or down is critical.

Engineers confront a similar problem when designing a new complex system and need to describe its behavior for which there is no closed-form solution or exhaustive analysis. This usually “leads to a tedious, time consuming, and detailed study of the engineering process in question, delaying the overall process of design and limiting the total number of possibilities that can be investigated. A set of simple and intuitive design laws based only on the most relevant parameters would be of enormous help in this case.”[2]

The underlying reasons for the wide applicability of power law models in engineering include the following:

• The combination of units has the form of a power law;
• The expressions of many physical phenomena have the form of power laws, as noted above; and
• Many empirical regressions of engineering data in log-log plots tend to give a straight line, which corresponds to a
• power law.

Scaling laws and the cost-to-capacity method are particularly useful in developing cost estimates for industrial plants or equipment where the scope is narrowly defined and the exact configuration and specific design are unknown. If performed correctly, the cost-to-capacity method can provide time-effective and reliable cost estimations to determine the feasibility of a design, optimal size or capacity, and aids in deciding what configuration and materials might be optimal. It is for these same reasons that scaling laws are a highly useful and practical tool for valuation professionals, along with other high-level empirical methods such as Nelson’s complexity indices for the refining and petrochemical industries.

With valuation opinions being essentially a judgment under conditions of uncertainty, it is important for such judgment to conform with the definition. The Merriam-Webster dictionary defines judgement as “a formal utterance of an authoritative opinion; the process of forming an opinion or evaluation by discerning and comparing.”[3] This implies that an opinion based on application of the cost-to-capacity method can be considered authoritative only when the appraiser or cost engineer understands and has investigated the nature of the scaling relationship and the limits of its application.

Scaling Exponents and Cost-to-Capacity Methodology

In the cost-to-capacity method, scaling exponents are applied to develop cost estimates. The cost-to-capacity method is a cost estimation tool that utilizes costs and capacities for existing facilities or pieces of machinery and equipment (“M&E”) to develop cost estimates for a planned or hypothetical facility or piece of M&E.[]4 This cost estimation method is governed by the concept that the costs of facilities or M&E of similar technology, but different size or capacity, vary nonlinearly. Specifically, cost is a function of size or capacity raised to a scaling exponent or scale factor.[5] The applicable equation is as follows:

The scaling exponent captures the nonlinear relationship that exists and economies of scale where, as a capacity of a facility or piece of M&E increases, the incremental cost decreases for each additional unit of capacity.[6]

The Association for the Advancement of Cost Engineering (“AACE”) International identifies five classes of costs estimates, from 1 through 5. Class 1 cost estimates are the most detailed and are based on a fully defined project scope, while Class 5 estimates are more preliminary in nature and are based on a project scope that is not fully defined. Costs developed by the cost-to-capacity method are considered Class 5 or Class 4 estimates according to AACE International.[7]

Scaling Exponent Principles

Costs associated with different capacity facilities or pieces of M&E do not all vary nonlinearly or experience economies of scale. A scaling exponent of less than 1 indicates that economies of scale exist and the incremental cost of the next added unit of capacity will cost less than the previous unit of capacity. When the scaling exponent is greater than 1, the opposite is true, i.e. the incremental cost increases for every added unit of capacity. A scaling exponent of exactly 1 indicates that a linear relationship between cost and capacity exists.[8] A scaling exponent of 1 may also indicate that it is just as economically feasible to build two small facilities as one large facility with the same capacity.[9]

It is important to note that one scaling exponent may not be applicable to all ranges of capacity for a facility or piece of M&E. In many cases, the scaling exponent increases at certain ranges of capacity due to fixed increases in costs for larger equipment sizes.[10] Scaling exponents can also vary between technologies and types of facilities or pieces of M&E based on numerous factors including but not limited to differences in materials costs, labor requirements, overhead, and market economics.[11]

The table below shows several scaling exponents for certain industrial facilities and M&E.

We briefly describe certain scaling relationships developed from the authors own research in order to help understand why certain exponents may differ. The following graph illustrates actual costs for mining trucks with various payloads. It represents a so-called super-linear relationship between the parameter of capacity (i.e., payload) and cost, with the scaling exponent being higher than 1, at 1.14.

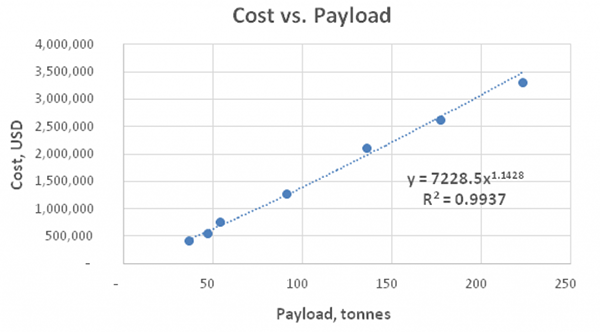
We have also found super-linear relationship between cost and capacity for both industrial trucks and cars. It may be attributed to the fact that as payload or engine power increases, all critical components also grow in complexity and hence, cost also increases. Additionally, high-power trucks or luxury vehicles often are produced in small lots, or sometimes made to order, which also explains why their costs may scale up disproportionally.

Another example represents an analysis of two-crank single-action presses for sheet metal stamping used in automotive plants. As shown in the graph below, this type of equipment scales with an exponent of 0.51, a sub-linear relationship which is more typical for industrial machinery.

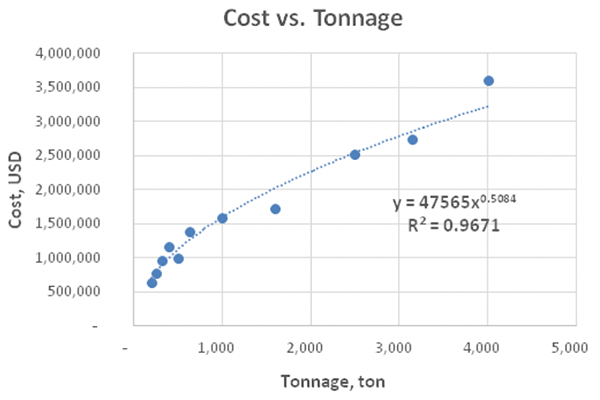
It is noteworthy that when performing graphical analysis for certain M&E, a power law scaling curve with a good fit may not exist, which may be attributed to the specific design of particular models.

Below are two graphs that depict additional examples of sub-linear scaling with various exponents and quality of fit. These graphs were developed as part of our research for cost versus capacity of several coal-fired and combined cycle natural gas–fired power plants in Central Europe.

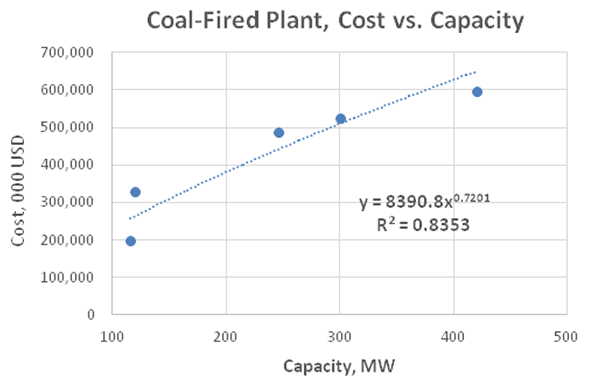
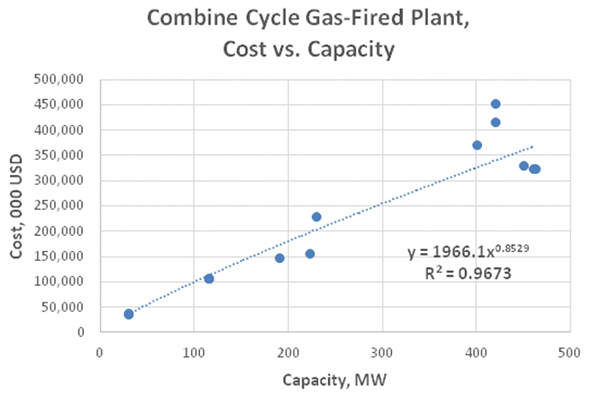
As indicated by the lower R^2 value, the above graph for the coal-fired plants reflects a wider variety of plant design related to the peculiarities of coal feed and ecological regulation requirements. Gas-fired plants may also differ depending on the type and manufacturer of turbines and generators. As would probably be expected, despite the economies of scale that are present for both types of power plant, the graphical analysis indicates they are more significant for coal-fired plants than for gas-fired plants. This conclusion is indicated by the lower scaling exponent for coal-fired plants of 0.7201, versus 0.8529 for the gas–fired plants.

Application and Considerations

There are several considerations to take into account prior to applying scaling exponents in the cost-to-capacity method. Appropriately addressing these factors will lead to more consistent and credible cost estimate results. Specifically, factors to consider prior to developing a cost-to-capacity analysis are as follows:

• The technology of the facility or M&E for which the cost is being estimated must be the same as, or very close to, that of the facility or M&E with a known historical cost.
• Different configurations or unique design or site characteristics may require a cost adjustment.
• Historical costs may need to be cost adjusted to the applicable date using indexes.
• Differences in location may require the application of a locational cost adjustment factor.
• The scaling exponent used must reflect the technology of both the facility or M&E for which the cost is being estimated and the facility or M&E with a known historical cost.
• The scaling exponent applied must be applicable to the range of capacities or sizes for the specific technology of the facility or M&E being analyzed.

Failing to consider even one of the above factors can result in non-credible cost estimate results. For example, assume that a preliminary cost estimate is to be developed for a planned industrial facility based on the known construction cost of an identical facility that was just completed in the same city. Virtually the only difference between the existing facility and the planned facility are their production capacities. To develop a reliable cost estimate in this scenario, the only one of the above factors that must be addressed is the use of an appropriate scaling exponent. Assume that without any appropriate research or due diligence, a scaling exponent of 0.70 is arbitrarily chosen for application in the analysis. The table on the following page depicts the inherent percent error in the cost estimate if the actual scaling exponent that is most appropriate to apply differs from 0.70.

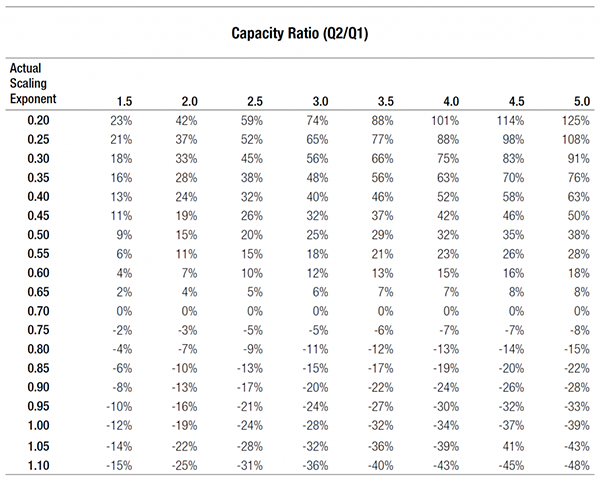
The above table shows that the use of an inappropriate scaling exponent can introduce significant error. Thus, the scaling exponent applied should be supported by publications or derivations in order to develop reliable cost estimation results.

Conclusion

If thoroughly researched and properly applied, cost-to-capacity formulas are an extremely useful and practical tool for appraisers and cost engineers engaged in developing replacement costs for various complex plants and production units. Key parameters and the specific design of particular facility, or individual piece of equipment for which a cost-to-capacity analysis is being applied must be analyzed. Ignoring unique attributes of the asset, or arbitrary selection of the scaling exponent, may result in a significant under- or overstatement of its replacement costs, while proper use of the method adds credibility to replacement cost opinions.

Endnotes

1. Xavier Gabaix, “Power Laws in Economics: An Introduction,” Journal of Economic Perspectives, Vol. 30, No. 1—Winter 2016, pp. 185–206.
2. Patricio F. Mendez, Department of Metallurgical and Materials Engineering, Colorado School of Mines, Golden, CO, and Fernando Ordóñez, Industrial and Systems Engineering, University of Southern California, Los Angeles, CA, Scaling Laws From Statistical Data and Dimensional Analysis, http://www-bcf.usc.edu/~fordon/docs/2005_jam_slaw.pdf
3. https://www.merriam-webster.com/dictionary/judgment
4. Richard K. Ellsworth, “Capacity Factor Cost Modeling for Gas-Fired Power Plants,” Construction Accounting & Taxation, Vol. 19, No. 1, Jan/Feb. 2009, p. 31.
5. Kenneth K. Humphreys, Jelen’s Cost and Optimization Engineering, McGraw-Hill, Inc., New York, NY, 1991, pp. 382-383, 386.
6. U.S. Department of Energy, National Energy Technology Laboratory, Office of Program Planning & Analysis, Performance Division, “Quality Guidelines for Energy Systems Studies, Capital Cost Scaling Methodology,” January 1, 2013, pp. 1-4. Retrieved from http://seca.doe.gov/energy-analyses/quality_guidelines.html.
7. AACE International Recommended Practice No. 17R-97, “Cost Estimate Classification System,” AACE International, Morgantown, WV, November 29, 2011, pp. 2-3.
8. Richard K. Ellsworth, “Cost to Capacity Factor Development for Facility Projects,” Cost Engineering, Vol. 49, No. 9, Sept. 2007, p. 27.
9. Larry R. Dysert, “Sharpen Your Cost Estimating Skills,” Cost Engineering, Vol. 45, No. 6, June 2003, p. 23.
10. 10David J. Chase, Modern Cost Engineering: Methods and Data, McGraw-Hill Publishing Co., New York, NY, pp. 228-229.
11. James R. Bielefeld Jr. and G. David Rucklos, “Cost Scaling Factors: How accurate are they?” Cost Engineering, Vol.34, No. 9, Oct. 1992, p. 16.
12. Kenneth K. Humphreys, Jelen’s Cost and Optimization Engineering, McGraw-Hill, Inc., New York, NY, 1991, pp. 392-393.

This article was previously published in the MTS Journal.